Despite the relentless pace of progress over the last half-century, there are still many problems that today’s computers can’t solve. Some simply await the next generation of semiconductors rounding the bend on the assembly line. Others will likely remain beyond the reach of classical computers forever. It is the prospect of finally finding a solution to these “classically intractable” problems that has CIOs, CTOs, heads of R&D, hedge fund managers, and others abuzz at the dawn of the era of quantum computing.
Their enthusiasm is not misplaced. In the coming decades, we expect productivity gains by end users of quantum computing, in the form of both cost savings and revenue opportunities, to surpass $450 billion annually. Gains will accrue first to firms in industries with complex simulation and optimization requirements. It will be a slow build for the next few years: we anticipate value for end users in these sectors to reach a relatively modest $2 billion to $5 billion by 2024. But value will then increase rapidly as the technology and its commercial viability mature. When they do, the opportunity will not be evenly distributed—far from it. Since quantum computing is a step-change technology with substantial barriers to adoption, early movers will seize a large share of the total value, as laggards struggle with integration, talent, and IP.
Based on interviews and workshops involving more than 100 experts, a review of some 150 peer-reviewed publications, and analysis of more than 35 potential use cases, this report assesses how and where quantum computing will create business value, the likely progression, and what steps executives should take now to put their firms in the best position to capture that value.
Who Benefits?
If quantum computing’s transformative value is at least five to ten years away, why should enterprises consider investing now? The simple answer is that this is a radical technology that presents formidable ramp-up challenges, even for companies with advanced supercomputing capabilities. Both quantum programming and the quantum tech stack bear little resemblance to their classical counterparts (although the two technologies might learn to work together quite closely). Early adopters stand to gain expertise, visibility into knowledge and technological gaps, and even intellectual property that will put them at a structural advantage as quantum computing gains commercial traction.
Quantum computing is a candidate for a precipitous breakthrough that may come at any time.
More important, many experts believe that progress toward maturity in quantum computing will not follow a smooth, continuous curve. Instead, quantum computing is a candidate for a precipitous breakthrough that may come at any time. Companies that have invested to integrate quantum computing into the workflow are far more likely to be in a position to capitalize—and the leads they open will be difficult for others to close. This will confer substantial advantage in industries in which classically intractable computational problems lead to bottlenecks and missed revenue opportunities.
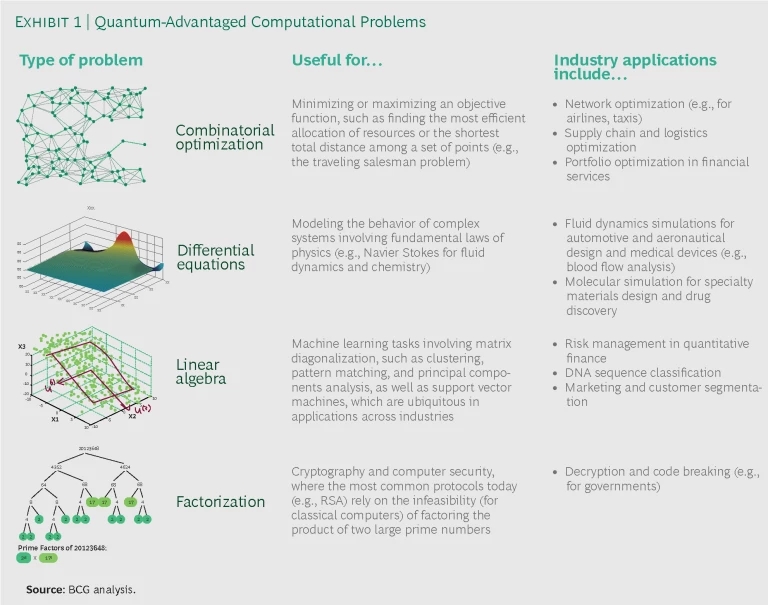
We have explored previously the likely development of quantum computing over the next ten years as well as The Coming Quantum Leap in Computing. (You can also take our quiz to test your own quantum IQ.) The assessment of future business value begins with the question of what kinds of problems quantum computers can solve more efficiently than binary machines. It’s far from a simple answer, but two indicators are the size and complexity of the calculations that need to be done.
Take drug discovery, for example. For scientists trying to design a compound that will attach itself to, and modify, a target disease pathway, the critical first step is to determine the electronic structure of the molecule. But modeling the structure of a molecule of an everyday drug such as penicillin, which has 41 atoms at ground state, requires a classical computer with some 1086 bits—more transistors than there are atoms in the observable universe. Such a machine is a physical impossibility. But for quantum computers, this type of simulation is well within the realm of possibility, requiring a processor with 286 quantum bits, or qubits.
This radical advantage in information density is why many experts believe that quantum computers will one day demonstrate superiority, or quantum advantage, over classical computers in solving four types of computational problems that typically impede efforts to address numerous business and scientific challenges. (See Exhibit 1.) These four problem types cover a large application landscape in a growing number of industries, which we will explore below.
Three Phases of Progress
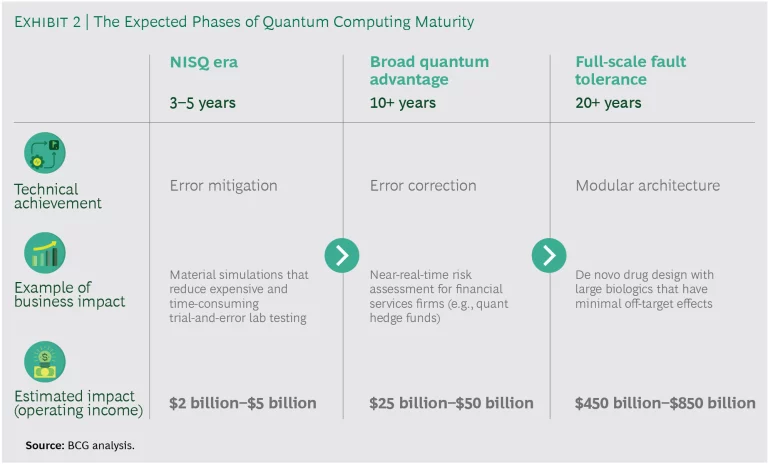
Quantum computing is coming. But when? How will this sea change play out? What will the impact look like early on, and how long will it take before quantum computers are delivering on the full promise of quantum advantage? We see applications (and business income) developing over three phases. (See Exhibit 2.)
The NISQ Era
The next three to five years are expected to be characterized by so-called NISQ (Noisy Intermediate-Scale Quantum) devices, which are increasingly capable of performing useful, discrete functions but are characterized by high error rates that limit functionality. One area in which digital computers will retain advantage for some time is accuracy: they experience fewer than one error in 1024 operations at the bit level, while today’s qubits destabilize much too quickly for the kinds of calculations necessary for quantum-advantaged molecular simulation or portfolio optimization. Experts believe that error correction will remain quantum computing’s biggest challenge for the better part of a decade.
That said, research underway at multiple major companies and startups, among them IBM, Google, and Rigetti, has led to a series of technological breakthroughs in error mitigation techniques to maximize the usefulness of NISQ-era devices. These efforts increase the chances that the near to medium term will see the development of medium-sized, if still error-prone, quantum computers that can be used to produce the first quantum-advantaged experimental discoveries in simulation and combinatorial optimization.
Broad Quantum Advantage
In 10 to 20 years, the period that will witness broad quantum advantage, quantum computers are expected to achieve superior performance in tasks of genuine industrial significance. This will provide step-change improvements over the speed, cost, or quality of a binary machine. But it will require overcoming significant technical hurdles in error correction and other areas, as well as continuing increases in the power and reliability of quantum processors.
In 10 to 20 years, quantum computers are expected to achieve superior performance in tasks of genuine industrial significance.
Quantum advantage has major implications. Consider the case of chemicals R&D. If quantum simulation enables researchers to model interactions among materials as they grow in size—without the coarse, distorting heuristic techniques used today—companies will be able to reduce, or even eliminate, expensive and lengthy lab processes such as in situ testing. Already, companies such as Zapata Computing are betting that quantum-advantaged molecular simulation will drive not only significant cost savings but the development of better products that reach the market sooner.
The story is similar for automakers, airplane manufacturers, and others whose products are, or could be, designed according to computational fluid dynamics. These simulations are currently hindered by the inability of classical computers to model fluid behavior on large surfaces (or at least to do so in practical amounts of time), necessitating expensive and laborious physical prototyping of components. Airbus, among others, is betting on quantum computing to produce a solution. The company launched a challenge in 2019 “to assess how [quantum computing] could be included or even replace other high-performance computational tools that, today, form the cornerstone of aircraft design.”
Full-Scale Fault Tolerance
The third phase is still decades away. Achieving full-scale fault tolerance will require makers of quantum technology to overcome additional technical constraints, including problems related to scale and stability. But once they arrive, we expect fault-tolerant quantum computers to affect a broad array of industries. They have the potential to vastly reduce trial and error and improve automation in the specialty-chemicals market, enable tail-event defensive trading and risk-driven high-frequency trading strategies in finance, and even promote in silico drug discovery, which has major implications for personalized medicine.
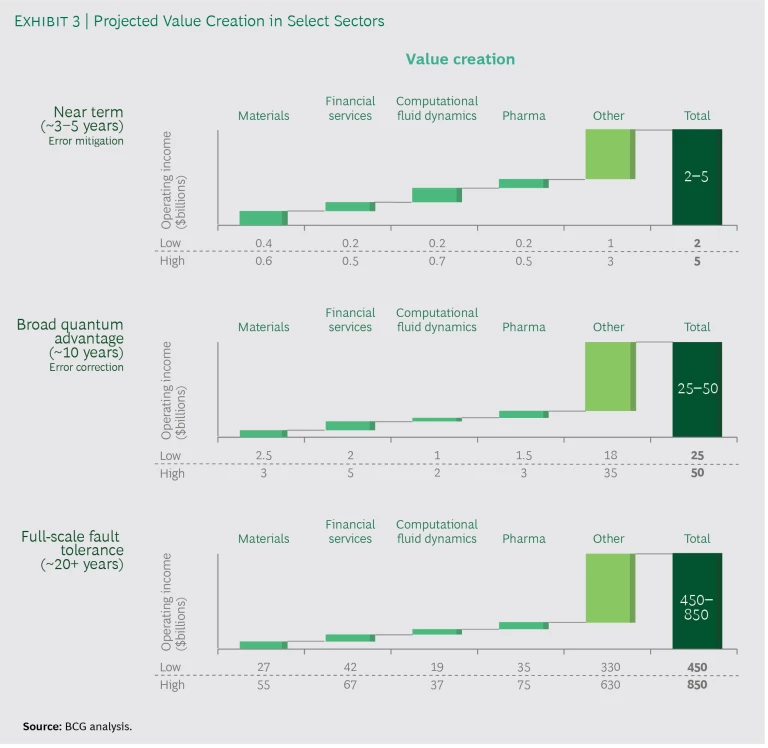
With all this promise, it’s little surprise that the value creation numbers get very big over time. In the industries we analyzed, we foresee quantum computing leading to incremental operating income of $450 billion to $850 billion by 2050 (with a nearly even split between incremental annual revenues streams and recurring cost efficiencies). (See Exhibit 3.) While that’s a big carrot, it comes at the end of a long stick. More important for today’s decision makers is understanding the potential ramifications in their industries: what problems quantum computers will solve, where and how the value will be realized, and how they can put their organizations on the path to value ahead of the competition.
How to Benefit
But what should companies do today to get ready? A good first step is performing a diagnostic assessment to determine the potential impact of quantum computing on the company or industry and then, if appropriate, developing a partnership strategy, ideally with a full-stack technology provider, to start the process of integrating capabilities and solutions. The first part of the diagnostic is a self-assessment of the company’s technical challenges and use of computing resources, ideally involving people from R&D and other functions, such as operations, finance, and strategy, to push boundaries and bring a full perspective to what will ultimately be highly technical discussions.
The key questions to ask are:
- Are you currently spending a lot of money or other resources to tackle problems with a high-performance computer? If so, do these efforts yield low-impact, delayed, or piecemeal results that leave value on the table?
- Does the presumed difficulty of solving simulation or optimization problems prevent you from trying high-performance computing or other computational solutions?
- Are you spending resources on inefficient trial-and-error alternatives, such as wet-lab experiments or physical prototyping?
- Are any of the problems you work on rooted in the quantum-advantaged problem archetypes identified above?
If the answer to any of these questions is yes, the next step is an “impact of quantum” (IQ) diagnostic that has two components. The first is sizing a company’s unsolved technical challenges and the potential quantum computing solutions as they are expected to develop and mature over time. The goal is to visualize the potential value of solutions that address real missed revenue opportunities, delays in time to market, and cost inefficiencies. This analysis requires combining domain-specific knowledge (of molecular simulation, for example) with expertise in quantum computing and then assessing potential future value. (We demonstrate how this is done at the industry level in the next section.) The second component of the IQ assessment is a vendor assessment. Given the ever-changing nature of the quantum computing ecosystem, it is critical to find the right partner or partner providers, meaning companies that have expertise across the broadest set of technical challenges that you face.
Some form of partnership will likely be the best play for enterprises wishing to get a head start on building a capability in the near term. A low-risk, low-cost strategy, it enables companies to understand how the technology will affect their industry, determine what skills and IT gaps they need to fill, and even play a role in shaping the future of quantum computing by providing technology providers with the industry-specific skills and expertise necessary to produce solutions for critical near-term applications.
Some form of partnership will likely be the best play for enterprises wishing to get a head start on building capability in the near term.
Partnerships have already become the model of choice for most of the commercial activity in the field to date. Among the collaborations formed so far are JPMorgan Chase and IBM’s joint development of solutions related to risk assessment and portfolio optimization, Volkswagen and Google’s work to develop batteries for electric vehicles, and the Dubai Electricity and Water Authority’s alliance with Microsoft to develop energy optimization solutions.
High-Impact Applications
One way to assess where quantum computing will have an early or outsized impact is to connect the quantum-advantaged problem types shown in Exhibit 1 with discrete pain points in particular industries. Behind each pain point is a bottleneck for which there may be multiple solutions or a latent pool of income that can be tapped in many ways, so the mapping must account for solutions rooted in other technologies—machine learning, for example—that may arrive on the scene sooner or at lower cost, or that may be integrated more easily into existing workflows. Establishing a valuation for quantum computing in a given industry (or for a given firm) over time—charting what we call a path to value—therefore requires gathering and synthesizing expertise from a number of sources, including:
- Industry business leaders who can attest to the business value of addressing a given pain point
- Industry technical experts who can assess the limits of current and future nonquantum solutions to the pain point
- Quantum computing experts who can confirm that quantum computers will be able to solve the problem and when
Using this methodology, we sized up the impact of quantum advantage on a number of sectors, with an emphasis on the early opportunities. Here are the results.
Materials Design and Drug Discovery
On the face of things, no two fields of R&D more naturally lend themselves to quantum advantage than materials design and drug discovery. Even if some experts dispute whether quantum computers will have an advantage in modeling the properties of quantum systems, there is no question that the shortcomings of classical computers limit R&D in these areas. Materials design, in particular, is a slow lab process characterized by trial and error. According to R&D Magazine, for specialty materials alone, global firms spend upwards of $40 billion a year on candidate material selection, material synthesis, and performance testing. Improvements to this workflow will yield not only cost savings through efficiencies in design and reduced time to market, but revenue uplift through net new materials and enhancements to existing materials. The benefits of design improvements yielding optimal synthetic routes also would, in all likelihood, flow downstream, affecting the estimated $460 billion spent annually on industrial synthesis.
The biggest benefit quantum computing offers is the potential for simulation, which for many materials requires computing power that binary machines do not possess. Reducing trial-and-error lab processes and accelerating discovery of new materials are only possible if materials scientists can derive higher-level spectral, thermodynamic, and other properties from ground-state energy levels described by the Schrödinger equation. The problem is that none of today’s approximate solutions—from Hartree-Fock to density functional theory—can account for the quantized nature of the electromagnetic field. Current computational approximations only apply to a subset of materials for which interactions between electrons can effectively be ignored or easily approximated, and there remains a well-defined set of problems in want of simulation-based solutions—as well as outsized rewards for the companies that manage to solve them first. These problems include simulations of strongly correlated electron systems (for high-temperature superconductors), manganites with colossal magnetoresistance (for high-efficiency data storage and transfer), multiferroics (for high-absorbency solar panels), and high-density electrochemical systems (for lithium air batteries).
No two fields of R&D more naturally lend themselves to quantum advantage than materials design and drug discovery.
All of the major players in quantum computing, including IBM, Google, and Microsoft, have established partnerships or offerings in materials science and chemistry in the last year. Google’s partnership with Volkswagen, for example, is aimed at simulations for high-performance batteries and other materials. Microsoft released a new chemical simulation library developed in collaboration with Pacific Northwest National Laboratory. IBM, having run the largest-ever molecular simulation on a quantum computer in 2017, released an end-to-end stack for quantum chemistry in 2018.
Potential end users of the technology are embracing these efforts. One researcher at a leading global materials manufacturer believes that quantum computing “will be able to make a quality improvement on classical simulations in less than five years,” during which period value to end users approaching some $500 million is expected to come in the form of design efficiencies (measured in terms of reduced expenditures across the R&D workflow). As error correction enables functional simulations of more complex materials, “you’ll start to unlock new materials and it won’t just be about efficiency anymore,” a professor of chemistry told us. During the period of broad quantum advantage, we estimate that upwards of $5 billion to $15 billion in value (which we measure in terms of increased R&D productivity) will accrue to end users, principally through development of new and enhanced materials. Once full-scale fault-tolerant quantum computers become available, value could reach the range of $30 billion to $60 billion, principally through new materials and extensions of in-market patent life as time-to-market is reduced. As the head of business development at a major materials manufacturer put it, “If unknown chemical relationships are unlocked, the current specialty market [currently $51 billion in operating income annually] could double.”
Quantum advantage in drug discovery will be later to arrive given the maturity of existing simulation methods for “established” small molecules. Nonetheless, in the long run, as quantum computers unlock simulation capabilities for molecules of increasing size and complexity, experts believe that drug discovery will be among the most valuable of all industry applications. In terms of cost savings, the drug discovery workflow is expected to become more efficient, with in silico modeling increasingly replacing expensive in vitro and in vivo screening. But there is good reason to believe that there will be major top-line implications as well. Experts expect more powerful simulations not only to promote the discovery of new drugs but also to generate replacement value over today’s generics as larger molecules produce drugs with fewer off-target effects. Between reducing the $35 billion in annual R&D spending on drug discovery and boosting the $920 billion in yearly branded pharmaceutical revenues, quantum computing is expected to yield $35 billion to $75 billion in annual operating income for end users once companies have access to fault-tolerant machines.
Financial Services
In recent history, few if any industries have been faster to adopt vanguard technologies than financial services. There is good reason to believe that the industry will quickly ramp up investments in quantum computing, which can be expected to address a clearly defined set of simulation and optimization problems—in particular, portfolio optimization in the short term and risk analytics in the long term. Investment money has already started to flow to startups, with Goldman Sachs and Fidelity investing in full-stack companies such as D-Wave, while RBS and Citigroup have invested in software players such as 1QBit and QC Ware.
Our discussions with quantitative investors about the pain points in portfolio optimization, arbitrage strategy, and trading costs make it easy to understand why. While investors use classical computers for all these problems today, the capabilities of these machines are limited—not so much by the number of assets or the number of constraints introduced into the model as by the type of constraints. For example, adding noncontinuous, nonconvex functions such as interest rate yield curves, trading lots, buy-in thresholds, and transaction costs to investment models makes the optimization “surface” so complex that classical optimizers often crash, simply take too long to compute, or, worse yet, mistake a local optimum for the global optimum. To get around this problem, analysts often simplify or exclude such constraints, sacrificing the fidelity of the calculation for reliability and speed. Such tradeoffs, many experts believe, would be unnecessary with quantum combinatorial optimization. Exploiting the probability amplitudes of quantum states is expected to dramatically accelerate portfolio optimization, enabling a full complement of realistic constraints and reducing portfolio turnover and transaction costs—which one head of portfolio risk at a major US bank estimates to represent as much as 2% to 3% of assets under management.
Income gains from portfolio optimization should reach about $400 million in the next three to five years and accelerate quickly.
We calculate that income gains from portfolio optimization should reach $200 million to $500 million in the next three to five years and accelerate swiftly with the advent of enhanced error correction during the period of broad quantum advantage. The resulting improvements in risk analytics and forecasting will drive value creation beyond $5 billion. As the brute-force Monte Carlo simulations used for risk assessment today give way to more powerful “quantum walk algorithms,” faster simulations will give banks more time to react to negative market risk (with estimated returns of as much as 12 basis points). The expected benefits include better intraday risk analytics for banks and near-real-time risk assessment for quantitative hedge funds.
“Brute-force Monte Carlo simulations for economic spikes and disasters took a whole month to run,” complained one former quantitative analyst at a leading US hedge fund. Bankers and hedge fund managers hope that, with the kind of whole-market simulations theoretically possible on full-scale fault-tolerant quantum computers, they will be able to better predict black-swan events and even develop risk-driven high-frequency trading. “Moving risk management from positioning defensively to an offensive trading strategy is a whole new paradigm,” noted one former trader at a US hedge fund. Coupled with enhanced model accuracy and positioning against extreme tail events, reductions in capital reserves (by as much as 15% in some estimates) will position quantum computing to deliver $40 billion to $70 billion in operating income to banks and other financial services companies as the technology matures.
Computational Fluid Dynamics
Simulating the precise flow of liquids and gases in changing conditions on a computer, known as computational fluid dynamics, is a critical but costly undertaking for companies in a range of industries. Spending on simulation software by companies using CFD to design airplanes, spacecraft, cars, medical devices, and wind turbines exceeded $4 billion in 2017, but the costs that weigh most heavily on decision makers in these industries are those related to expensive trial-and-error testing such as wind tunnel and wing flex tests. These direct costs, together with the revenue potential of energy-optimized design, have many experts excited by the prospect of introducing quantum simulation into the workflow. The governing equations behind CFD, known as the Navier-Stokes equations, are nonlinear partial differential equations and thus a natural fit for quantum computing.
The first bottleneck in the CFD workflow is actually an optimization problem in the preprocessing stage that precedes any fluid dynamics algorithms. Because of the computational complexity involved in these algorithms, designers create a mesh to simulate the surface of an object—say, an airplane wing. The mesh is composed of geometric primitives whose vertices form a constellation of nodes. Most classic optimizers impose a limit on the number of nodes in a mesh that can be simulated efficiently to 109. This forces the designer into a tradeoff between how fine-grained and how large a surface can be simulated. Quantum optimization is expected to relieve the designer of that constraint so that bigger pieces of the puzzle can be solved at once and more accurately—from the spoiler, for example, to the entire wing. Improving this preprocessing stage of the design process is expected to lead to operating-income gains of between $1 billion and $2 billion across industries through reduced costs and faster revenue realization.
We expect value creation in the phase of full-scale fault tolerance to range from $19 billion to $37 billion in operating income.
As quantum computers mature, we expect the benefits of improved mesh optimization to be surpassed by those from accelerated and improved simulations. As with mesh optimization, the tradeoff in fluid simulations is between speed and accuracy. “For large simulations with more than 100 million cells,” one of our own experts told us, “run times could be weeks even on very powerful supercomputers.” And that is with the use of simplifying heuristics, such as approximate turbulence models. During the period of broad quantum advantage, experts believe that quantum simulation could enable designers to reduce the number of heuristics required to run Navier-Stokes solvers in manageable time periods, resulting in the replacement of expensive physical testing with accurate moving-ground aerodynamic models, unsteady aerodynamics, and turbulent-flow simulations. The benefits to end users in terms of cost reductions are expected to start at $1 billion to $2 billion during this period. With full-scale fault tolerance, value creation could as much as triple, as experts anticipate that quantum linear solvers will unlock predictive simulations that not only obviate physical testing requirements but lead to product improvements (such as improved fuel economy) and manufacturing yield optimization as well. We expect value creation in the phase of full-scale fault tolerance to range from $19 billion to $37 billion in operating income.
Other Industries
During the NISQ era, we expect more than 40% of the value created in quantum computing to come from materials design, drug discovery, financial services, and applications related to CFD. But applications in other industries will show early promise as well. Examples include:
- Transportation and Logistics. Using quantum computers to address inveterate optimization challenges (such as the traveling salesman problem and the minimum spanning tree problem) is expected to lead to efficiencies in route optimization, fleet management, network scheduling, and supply chain optimization.
- Energy. With the era of easy-to-find oil and gas coming to an end, companies are increasingly reliant on wave-based geophysical processing to locate new drilling sites. Quantum computing could not only accelerate the discovery process but also contribute to drilling optimizations for both greenfield and brownfield operations.
- Meteorology. Many experts believe that quantum simulation will improve large-scale weather and climate forecasting technologies, which would not only enable earlier storm and severe-weather warnings but also bring speed and accuracy gains to industries that depend on weather-sensitive pricing and trading strategies.
Should quantum computing become integrated into machine learning workflows, the list of affected industries would expand dramatically, with salient applications wherever predictive capabilities (supervised learning and deep learning), principal component analysis (dimension reduction), and clustering analysis (for anomaly detection) provide an advantage. While experts are divided on the timing of quantum computing’s impact on machine learning, the stakes are so high that many of the leading players are already putting significant resources against it today, with promising early results. For example, in conjunction with researchers from Oxford and MIT, a group from IBM recently proposed a set of methods for optimizing and accelerating support vector machines, which are applicable to a wide range of classification problems but have fallen out of favor in recent years because they quickly become inefficient as the number of predictor variables rises and the feature space expands. The eventual role of quantum computing in machine learning is still being defined, but early theoretical work, at least for optimizing current methods in linear algebra and support vector machines, shows promise.
While it may be years before investments in a quantum strategy begin to pay off, failure to understand the coming impact of quantum computing in one’s industry is at best a missed opportunity, at worst an existential mistake. Companies that stay on the sidelines, assuming they can buy their way into the game later on, are likely to find themselves playing catchup—and with a lot of ground to cover.